Jaime Alvarez Benayas
2021-03-13 13:14:04 UTC
Hello.
I am having problems understanding what criteria are used to determine relationship redundancy for a "circle" of relationships between 3 entities in the entity - relationship model.
I am adding the link to my stackoverflow question copied here:
https://stackoverflow.com/questions/66613891/criteria-for-considering-redundant-relationships-in-entity-relationship-diagra
I was starting with the following example: Course - department - teacher relationships.
Loading Image...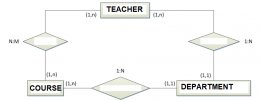
My criteria to declare a relationship (A -> C) as non redundant (can NOT be inferred from A -> B -> C) is either:
1) A -> B has minimum cardinality 0 (ie. 1 element of A can be associated with 0 elements of B), since then, B can't be determined (and therefore C can't be determined). OR
2) If A -> B and B -> C have a maximum cardinality of N (ie. 1 element of A can be associated with N elements of B and 1 element of B can be associated with N elements of C simultaneously). My assumption for this is that knowing the elements of B associated with A and knowing the elements of C associated with B can't be used to know one specific A -> C.
I consider the above "both ways": A -> B -> C and C -> B -> A. If going any way I get any of the above, I consider the relationship is NOT redundant since A -> C can't be inferred from A -> B -> C. I am assuming this, regardless of the cardinality between the candidate redundant relationship A -> C.
Given my assumptions, I consider the example [Course (C) - department (D) - teacher (T)]. I deduce that the only relationship which is redundant is between course and teacher since:
T -> C: T -> (1,1) D -> (1,n) C [Cardinality shown in parenthesis]. Which allows to deduce T -> C from T -> D -> C.
C -> T: C -> (1,1) D -> (1,n) T. Which allows to deduce C -> T from C -> D -> T.
However, in the example given, the redundant relationship is Teacher and Department. The reasoning is that if the courses a teacher teaches are known and the department to which each course belongs is also known, it can be deduced to what department belongs each teacher. Also, given a department, if we know its courses, and we know the teachers who teach the courses we will know the teachers associated with department.
With my criteria, I don't see how this is the case, since: D -> T: D -> (1,n) C -> T (1,n). This complies with point 2) above and therefore D -> T can't be deduced from D -> C -> T.
There is also another example with the same relationships but different cardinality (shown in red), this is where I got my criteria from:
Loading Image...
In this case, it is specified that there are no redundant relationships, for the following reasons:
T - D:
If we know the courses taught by a teacher, and the departments to which the courses are assigned, Do we know which department the professor belongs to? NO, since the course can be assigned to several departments. This is where I deduced my criteria: T -> D: T -> (0,n) C -> (1,n) D. We have two 1->N relationships, therefore it is non-redundant.
Also it says: what if a course was only attached to a Department? Still, a teacher may not teach any courses, then we couldn't know his/her department. Which is my other criteria:
T -> (0,n) C [minimum cardinality of 0, we can't know C in some cases, and therefore, we can't know D.
It also adds: given a department, if we know its courses, and we know the teachers who teach the courses, we will know the professors associated with the department.
1) T - C: A course can be assigned to several departments, and these may have several teachers, then you can not know the teacher concrete that the course teaches. Ie. We have two 1-N relationships: C -> (1,n) D -> (1,n) T. Therefore, it is non-redundant.
2) C - D: Given a course taught by a teacher, and he/she belonging to a department, we cannot know what other departments have associated the course. I am assuming: D -> (1,n) P -> (0,n) C. We have two 1-N relationships therefore, it is non-redundant.
Finally I have a third example with Author (A), Editorial (E) and Book (B) as follows:
Loading Image...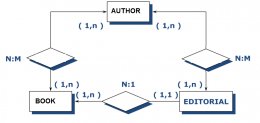
I am told that the redundant relationship is Author - Editorial. However, I am finding no redundant relationships as per my criteria since they have two 1:N relationships:
E -> A: E -> (1,n) B -> (1,n) A
B -> E: B -> (1,n) A -> (1,n) E
A -> B: A -> (1,n) E -> (1,n) B.
Thank you for taking the time to read until here. Are my criteria wrong? If so, what criteria should I use to consider a relationship redundant?
I am having problems understanding what criteria are used to determine relationship redundancy for a "circle" of relationships between 3 entities in the entity - relationship model.
I am adding the link to my stackoverflow question copied here:
https://stackoverflow.com/questions/66613891/criteria-for-considering-redundant-relationships-in-entity-relationship-diagra
I was starting with the following example: Course - department - teacher relationships.
Loading Image...
My criteria to declare a relationship (A -> C) as non redundant (can NOT be inferred from A -> B -> C) is either:
1) A -> B has minimum cardinality 0 (ie. 1 element of A can be associated with 0 elements of B), since then, B can't be determined (and therefore C can't be determined). OR
2) If A -> B and B -> C have a maximum cardinality of N (ie. 1 element of A can be associated with N elements of B and 1 element of B can be associated with N elements of C simultaneously). My assumption for this is that knowing the elements of B associated with A and knowing the elements of C associated with B can't be used to know one specific A -> C.
I consider the above "both ways": A -> B -> C and C -> B -> A. If going any way I get any of the above, I consider the relationship is NOT redundant since A -> C can't be inferred from A -> B -> C. I am assuming this, regardless of the cardinality between the candidate redundant relationship A -> C.
Given my assumptions, I consider the example [Course (C) - department (D) - teacher (T)]. I deduce that the only relationship which is redundant is between course and teacher since:
T -> C: T -> (1,1) D -> (1,n) C [Cardinality shown in parenthesis]. Which allows to deduce T -> C from T -> D -> C.
C -> T: C -> (1,1) D -> (1,n) T. Which allows to deduce C -> T from C -> D -> T.
However, in the example given, the redundant relationship is Teacher and Department. The reasoning is that if the courses a teacher teaches are known and the department to which each course belongs is also known, it can be deduced to what department belongs each teacher. Also, given a department, if we know its courses, and we know the teachers who teach the courses we will know the teachers associated with department.
With my criteria, I don't see how this is the case, since: D -> T: D -> (1,n) C -> T (1,n). This complies with point 2) above and therefore D -> T can't be deduced from D -> C -> T.
There is also another example with the same relationships but different cardinality (shown in red), this is where I got my criteria from:
Loading Image...
In this case, it is specified that there are no redundant relationships, for the following reasons:
T - D:
If we know the courses taught by a teacher, and the departments to which the courses are assigned, Do we know which department the professor belongs to? NO, since the course can be assigned to several departments. This is where I deduced my criteria: T -> D: T -> (0,n) C -> (1,n) D. We have two 1->N relationships, therefore it is non-redundant.
Also it says: what if a course was only attached to a Department? Still, a teacher may not teach any courses, then we couldn't know his/her department. Which is my other criteria:
T -> (0,n) C [minimum cardinality of 0, we can't know C in some cases, and therefore, we can't know D.
It also adds: given a department, if we know its courses, and we know the teachers who teach the courses, we will know the professors associated with the department.
1) T - C: A course can be assigned to several departments, and these may have several teachers, then you can not know the teacher concrete that the course teaches. Ie. We have two 1-N relationships: C -> (1,n) D -> (1,n) T. Therefore, it is non-redundant.
2) C - D: Given a course taught by a teacher, and he/she belonging to a department, we cannot know what other departments have associated the course. I am assuming: D -> (1,n) P -> (0,n) C. We have two 1-N relationships therefore, it is non-redundant.
Finally I have a third example with Author (A), Editorial (E) and Book (B) as follows:
Loading Image...
I am told that the redundant relationship is Author - Editorial. However, I am finding no redundant relationships as per my criteria since they have two 1:N relationships:
E -> A: E -> (1,n) B -> (1,n) A
B -> E: B -> (1,n) A -> (1,n) E
A -> B: A -> (1,n) E -> (1,n) B.
Thank you for taking the time to read until here. Are my criteria wrong? If so, what criteria should I use to consider a relationship redundant?